반응형
확률적 경사하강법(SGD)
Preview
- 이전의 배운 경사하강법은 전체 데이터를 모두 사용하여 기울기를 계산 → 많은 시간 필요
- 이러한 단점을 보완하기 위해 확률적 경사하강법 사용 (데이터를 랜덤 샘플링하여 계산
GD
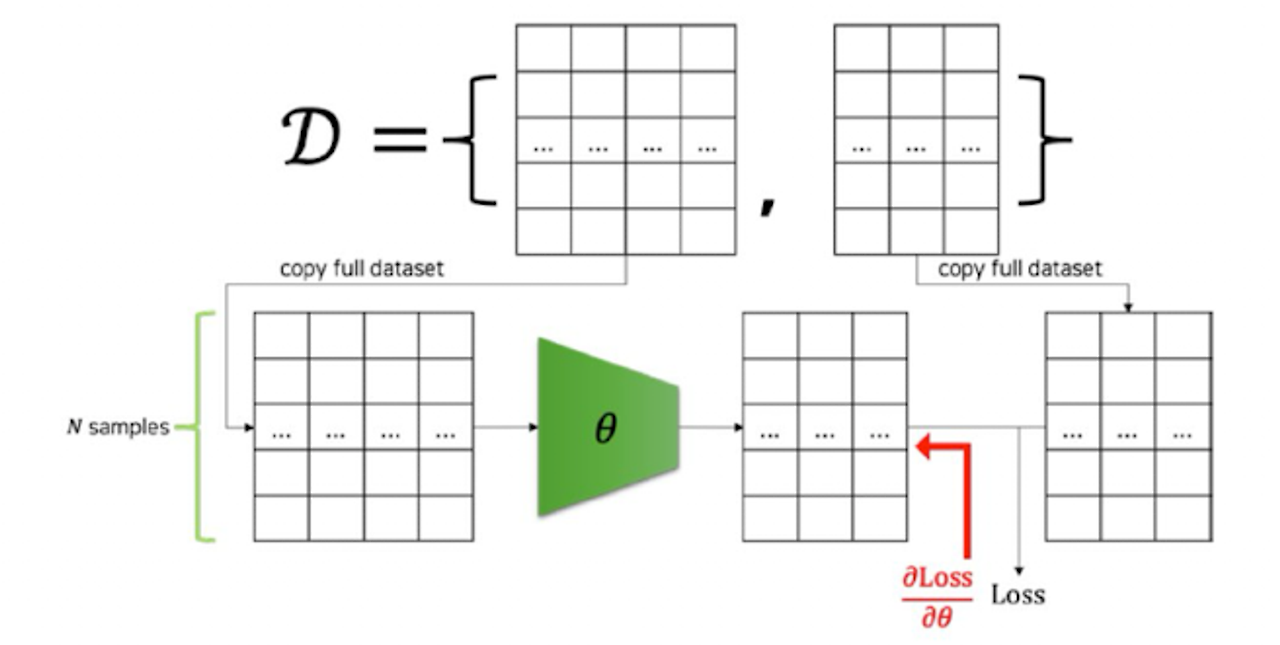
- 파라미터를 업데이트하기 위해 전체 데이터셋을 모델에 통과시키고
- 손실 값을 가중치 파라미터로 미분하여 파라미터 업데이트
→ 비효율적 (메모리 한계, 학습 속도 문제)
SGD
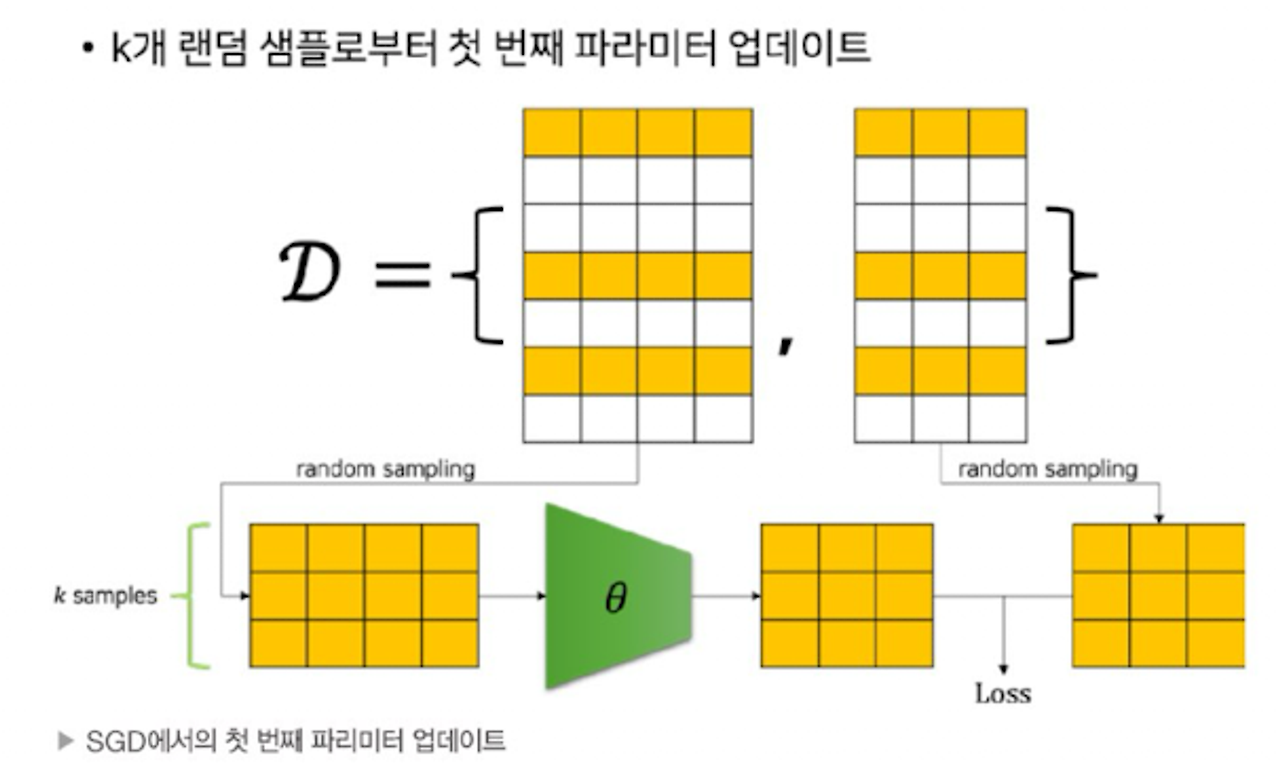
- 전체 데이터셋에서 랜덤 샘플링하여 모델에 통과시켜 손실값 계산→ 파라미터 업데이트
- 비복원 추출
- 전체 데이터셋의 샘플들이 전부 모델의 통과하는 것 : 에포크
- 한 개의 미니배치를 모델에 통과 시키는 것 : 이터레이션
- 아래 수식은 미니배치 크기를 k라고 할 때 이터레이션, 에포크 횟수, 관계 (데이터 크키 N)
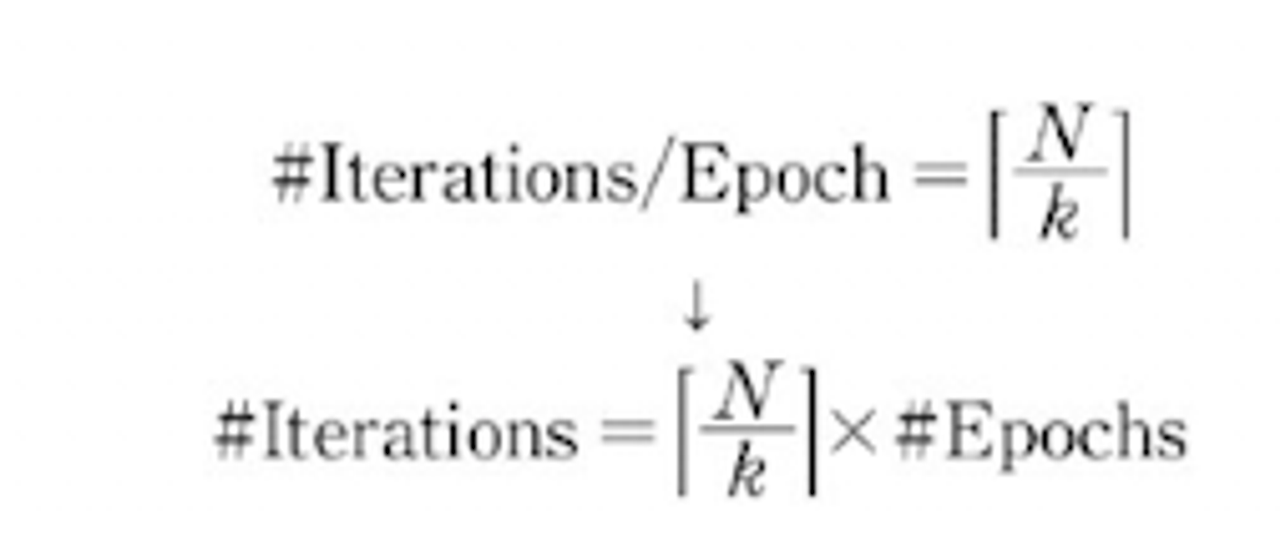
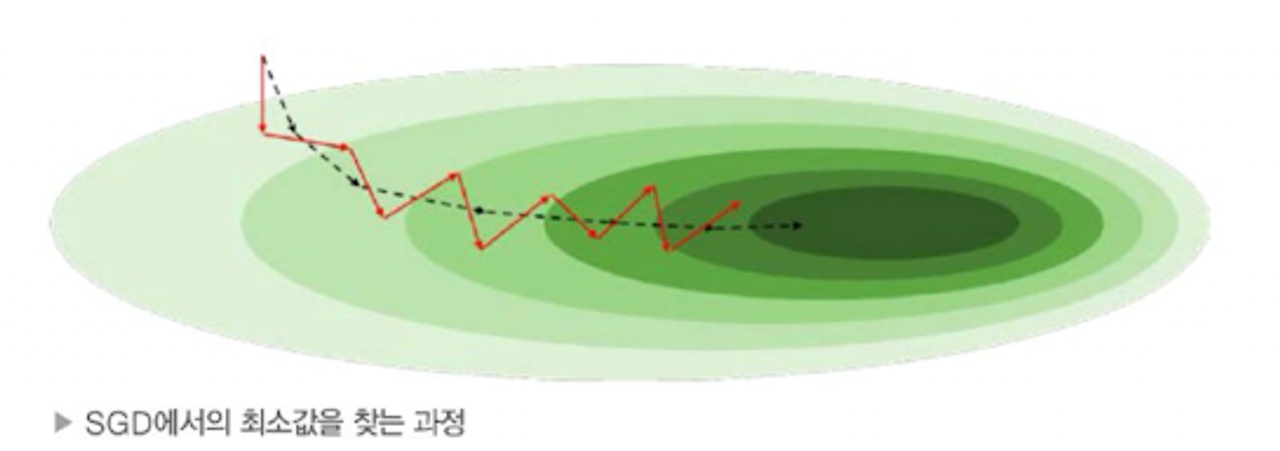
- 미니배치는 전체 데이터셋에서 랜덤 샘플링 되었기 떄문에 편향이 생김
- 미니배치를 통해 구성한 손실함수는 전체 데이터셋의 손실함수 모양과 다름
- 따라서 미분시 기울기 방향과, 모양이 다름
- 미니배치크기가 크면 → 계산량 증가, 미니 배치 크기 작아지면 → 편향이 커진다 → 지역 최소점은 탈출 가능
- 미니배치 또한 학습률과 같이 중요한 하이퍼파라미터 보통은 256 정도 크기에서 시작
최적화
- 모델의 가중치 파라미터는 경사하강법을 통해 데이터를 기반으로 자동으로 최적화 됨
- 하이퍼파라미터는 모델의 성능에 영향을 끼치지만, 자동으로 최적화 되지 않음
→ 최적의 하이퍼파라미터를 경험적 또는 휴리스틱한 방법을 통해 찾게 됨
학습률의 크기에 따른 특성과 동적 학습률의 필요성
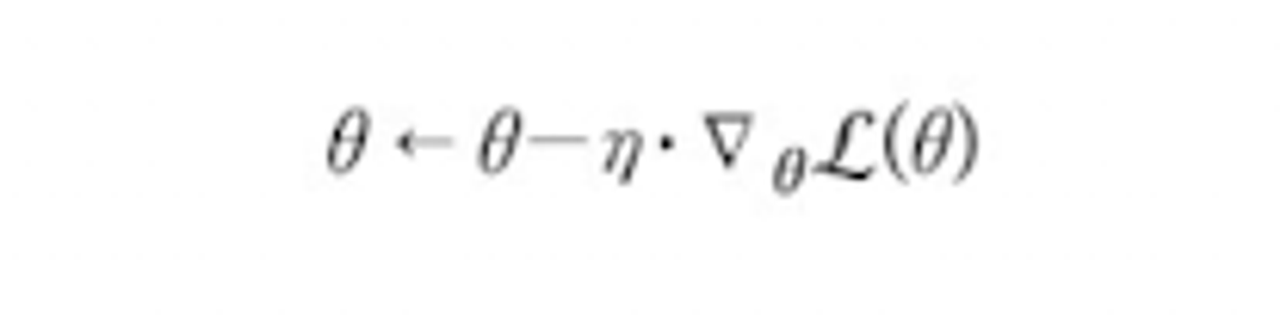
- 기존 파라미터에서 학습률(에타)를 곱해주어 파라미터가 변화하는 양 조절
- 학습률의 크기에 따라 학습 진행 양상 다름
- 학습률이 큰 경우 손실 값이 발산(왼쪽사진)
- 손실값이 작은 경우 학습 시간이 더디거나, local minima에 빠질 수 있음(오른쪽 사진)
→ 학습 초반에 학습률을 크게 하고 학습이 진행담에 따라 점점 더 학습률을 작게하면 어떨까?
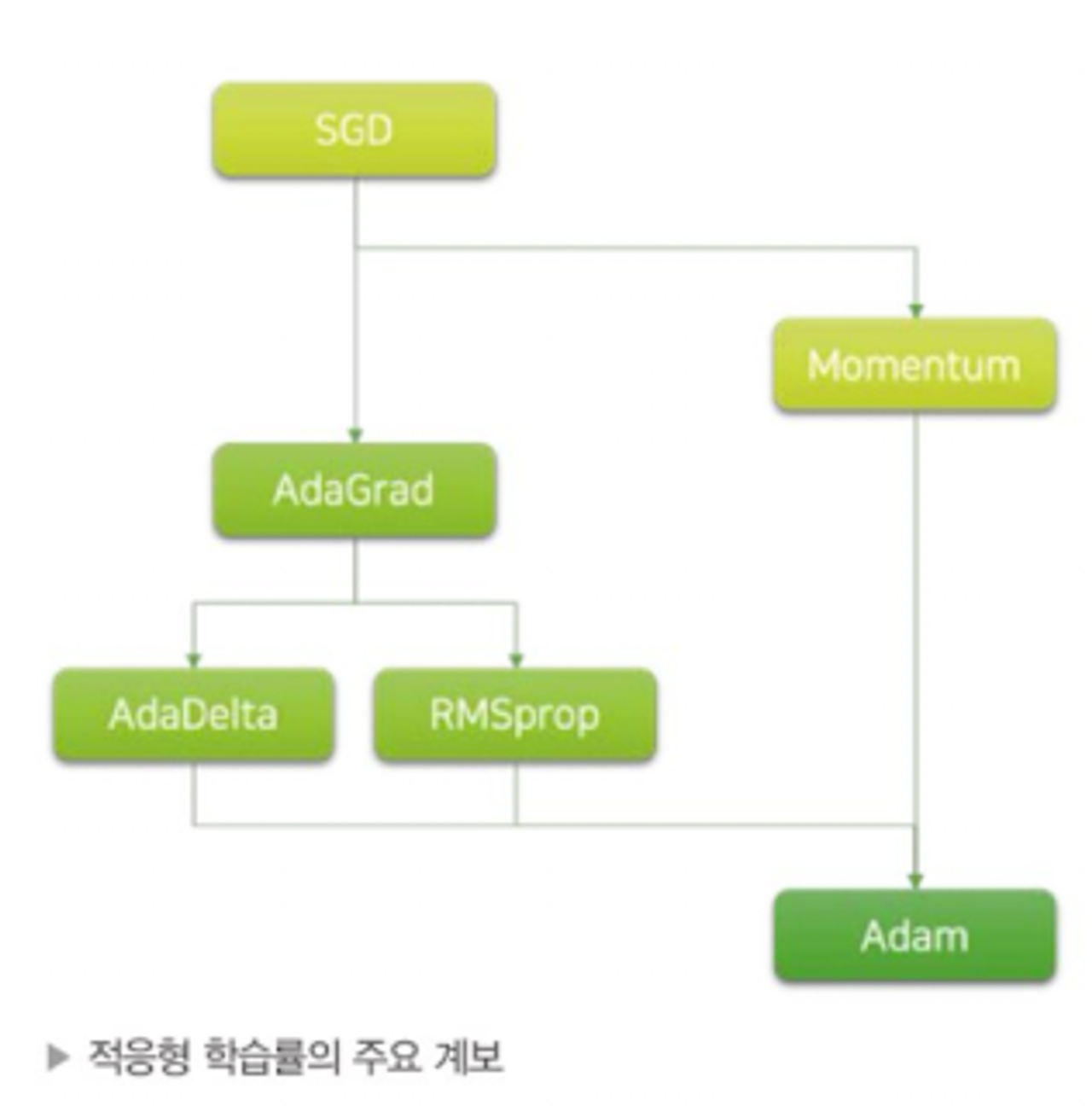
- 다양한 적응형 학습률에 대한 알고리즘이 있다. → 가장 많이 쓰이는 알고리즘은 아담(Adam)
아담의 기반이 되는 기초 알고리즘 부터 하나씩 다뤄보자
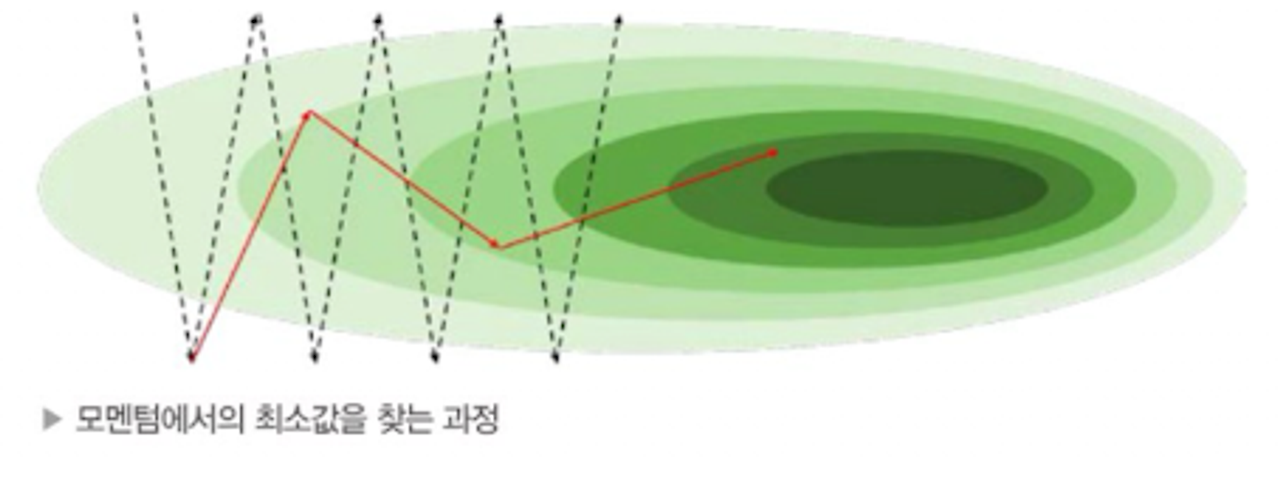
모멘텀
- 모멘텀은 시작부터 매번 계산된 그래디언트를 누적하는 형태
학습률 스케줄링
- 학습 초반은 어차피 갈길이 멀기 때문에 학습률을 크게, 학습 후반에 갈수록 미세한 가중치 파라미터 조정이 필요할 수 있기 때문에 학습률을 작게하는것이 어떨까
- 작은 학습률 시작 → 초반에 더딘 진행
- 큰 학습률 시작 → 미세한 파라미터 조정 어려움
→ 학습률 스케줄링 기법 활용 but, 하이퍼 파라미터가 더 추가되는 아쉬움이 생길 수 있음
아다그래드 옵티마이저
- 최초로 제안된 적응형 학습률 알고리즘
- 각 가중치 파라미터의 학습률은 가중치 파라미터가 업데이트될수록 반비례하여 작아짐
- 문제 : 파라미터 업데이트가 많이 될 경우 학습률이 너무 작아져 이후에 그래디언트가 크더라도 업데이트가 잘 이뤄지지 않을 수 있음
아담 옵티마이저
- 아다그래드 이후 알고리즘
- 기존 적응형 학습률 방식에 모멘텀(관성)이 추가된 알고리즘
- 가장 보편적으로 쓰이는 알고리즘
반응형
'Deep Learning' 카테고리의 다른 글
| 로컬 GPU 코랩에 연결하기 (Jupyter notebook) (0) | 2024.06.10 |
|---|---|
| 윈도우10에 딥러닝 환경 구축의 모든 것.. 이고 싶어요(tensorflow, GPU, CUDA, cudnn) (1) | 2024.06.10 |
| [cs231] SGD, SGD 모멘텀, AdaGrad, Adam 7강 (0) | 2024.04.29 |
| [DL] 클러스터링 (0) | 2024.04.25 |
| [DL] L1, L2 규제와 차원 축소 (0) | 2024.04.17 |



